top of page

Evaluating Expressions


Algebraic Expression: An expression that is composed of variables and/or numerals. The expression may also include grouping symbols and/or operation signs. Expressions do not contain an equality sign.
Variable: A letter that represents an unknown number.
Constant: A number that never changes.
Evaluate: To replace each of the variables in an expression with a number and calculate the result.
Value: The final number resulting from evaluating an expression.


Coefficient: A number that multiplies a variable.
If the coefficient of a variable is negative one, it can be represented by a negative sign directly in front of the variable.

Terms: The components of an algebraic expression. Terms can be numbers, variables, products of numbers and/or variables, and quotients of numbers and/or variables.

Like Terms: Terms that contain the same variable(s) raised to the same power(s).

Simplifying: Creating a simpler, equivalent expression by combining like terms, canceling common factors, combining and simplifying fractions, and applying the distributive, associative, and commutative laws.
The Commutative and Associative Laws

The commutative and associative laws are used to simplify and rearrange expressions.
Solving Equations


Equation: A number sentence with an equality sign between two expressions.
Solution: Any replacement for a variable that makes an equation or inequality true.

When canceling a coefficient that is a fraction, it can either be divided by itself or multiplied by its reciprocal.

Like terms should be combined before solving an equation. If like terms are on the same side, combine them. If like terms are on both sides, move one over, then combine.

Every equation can be classified into one of three equation types: identity, contradiction, or conditional.
Identity: An equation that is true for all replacements.
Contradiction: An equation that is never true.
Conditional: An equation that is true for some replacements.
Solution Set: The collection of all solutions.

Formula: An equation that utilizes numbers and/or letters to represent the relationship between two or more quantities.
Solving Inequalities

Inequality: A mathematical sentence using ≤ , ≥ , < , > , or ≠.
The same steps used to solve equations are used to solve inequalities.
.png)
When multiplying or dividing both sides of an inequality by a negative number, the direction of the inequality sign is flipped.

The > and < inequality symbols are graphed with an open circle to indicate that the endpoint is not a solution. The ≥ and ≤ symbols are graphed with a closed circle to indicate that the endpoint is a solution.

A variable can also be located between two inequality symbols.
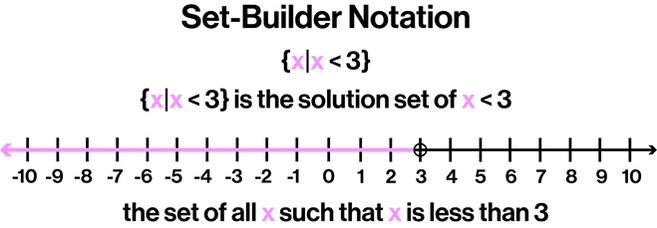
Set-Builder Notation: A solution set is named by describing the characteristics of its elements.

Interval Notation: A solution set is represented by a pair of numbers inside parentheses (> and <) and/or brackets [≥ and ≤]. When graphing inequalities, brackets and parentheses can be used instead of circles.

Word Problems


When working with word problems, certain key words can indicate a specific operation, inequality, or equality.
Coordinate Plane

Coordinate Plane: A plane that is used to graph points, lines, or curves. A coordinate plane is composed of a horizontal number line, the first axis, and a vertical number line, the second axis.

Axes: Two perpendicular number lines that are used to identify points in a plane.
Origin: The point (0 , 0) on a coordinate plane. The origin is the location where the two axes intersect.



Ordered Pair: A pair of numbers in the form (x , y).
Coordinates: The numbers in an ordered pair.
Abscissa: The first coordinate. The abscissa determines the horizontal distance from the origin.
Ordinate: The second coordinate. The ordinate determines the vertical distance from the origin.
The variables x and y are typically used when graphing on a plane.

Quadrants: The four regions of a coordinate plane. Coordinates within each quadrant carry different signs.


A coordinate plane allows you to visualize the solutions to an equation. Each solution is shown as a specific point on the plane.
Linear Equation: Equations that contain two variables, have a graph that is a straight line, and are in the form of y=mx+b or Ax+By=C.
When graphing a linear equation, at least three points are typically plotted with a straight line passing through each point.

y-axis: The vertical axis.
x-axis: The horizontal axis.
y-intercept: The point at which a graph crosses the y-axis.
x-intercept: The point at which a graph crosses the x-axis.


Slope: The ratio of the vertical change to the horizontal change for two points on a line. A line with a positive slope slants up from left to right, and a line with a negative slope slants down from left to right. The larger the absolute value of the slope, the steeper the line.
It does not matter which ordered pair is assigned (x1, y1) or (x2 , y2); the slope will be the same regardless.


Horizontal Line: A line with a slope of zero.
Vertical Line: A line with a slope that is undefined.


Excluding vertical and horizontal lines, there are three common forms of linear equations.

Lines are parallel if they have the same slope and do not intersect each other.

Lines are perpendicular if the product of their slopes is negative one or if one line is horizontal and the other is vertical. To find a perpendicular line, calculate the negative reciprocal of the given line’s slope.

Rate: A ratio that shows how two quantities change with respect to each other. Rates can be visualized using a coordinate plane.
Interpolation: Estimating a value between given values.
Extrapolation: Estimating a value beyond the given data.
Polynomials

Monomial: A variable, a constant, or the product of a constant and one or more variables. Monomials do not include division by a variable.

Polynomial: A monomial or a sum of monomials.

Terms of the Polynomial: Each monomial that makes up a polynomial.
Binomial: A polynomial with two terms.
Trinomial: A polynomial with three terms.

Degree of a Monomial: The number of variable factors in the monomial.

Leading Term: The term with the highest degree.
Leading Coefficient: The coefficient of the leading term.
The Degree of the Polynomial: The degree of the leading term.

Descending Order: The terms of a polynomial are arranged according to degree, from greatest to least. Descending order is the standard way polynomials are written.

Like terms within polynomials should be combined.

Polynomials can be evaluated if each variable is replaced with a number.

To add polynomials, use the commutative, associative, and distributive laws.

To subtract polynomials, change the subtrahend to its opposite and add.

To multiply monomials, multiply the coefficients and use the product rule for exponents on the variables.

To multiply a monomial by a polynomial, the distributive law is used.

To multiply polynomials, the distributive law is used multiple times.

The FOIL method can be used to multiply binomials.

The product of the sum and the difference of the same two terms can be simplified.

The square of a binomial can be simplified.

To divide a polynomial by a monomial, the quotient rule is used.

To divide a polynomial by a binomial, long division is used.

After performing a polynomial operation, the result can be checked by substituting values for the variables in both the original expression and the new expression. If the outputs are equal, the operation was completed correctly.
Factoring Polynomials

Factoring: To find an equal expression that is a product of the polynomial.
To factor a monomial, we find monomials whose product is the same as the original monomial.
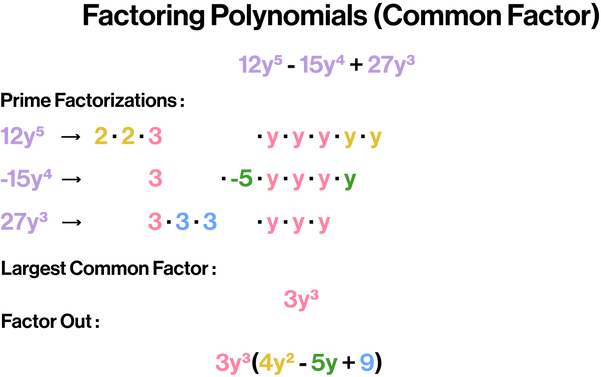
Largest Common Factor of a Polynomial: The largest common factor of the variables in all terms times the largest common factor of the coefficients. Prime factorization can be used to find the largest common factor. Unlike the greatest common factor, the largest common factor can be negative.
If the terms of a polynomial have a common factor, the largest common factor is factored out.

Factoring by Grouping: The polynomial is factored by splitting terms into groups that share a common factor. This method is used on polynomials with four or more terms.



Nonprime trinomials with a coefficient of one can be factored into two binomials.

Prime Polynomial: A polynomial that cannot be factored using rational numbers.

To factor some polynomials completely, more than one factoring method may be required.


Nonprime trinomials with a leading coefficient other than one can be factored using the FOIL method.

Nonprime trinomials with a leading coefficient other than one can be factored by grouping.


A unique property is used to factor perfect square trinomials.


A unique property is used to factor differences of squares; however, there is no general equation to factor sums of squares.



A unique property is used to factor the sums or differences of cubes.



Quadratic Equation: An equation of the form ax^2 + bx + c. Quadratic equations can be solved by factoring and applying the principle of zero products. Graphing is a method used to confirm a quadratic equation’s solutions.
Rational Expressions

Rational Expressions: Expressions that can be written as the quotient of two polynomials.

Any replacement values that result in the denominator equaling zero must be avoided.

Rational expressions are simplified by first factoring the numerator and/or the denominator and then canceling out any common factors.

To multiply rational expressions, combine the rational expressions so they share a fraction bar, factor, then simplify.

To divide rational expressions, multiply by the reciprocal.

To add rational expressions with the same denominator, add the numerators, factor, and then simplify.

To subtract rational expressions with the same denominator, convert the subtrahend to its opposite, add, factor, and then simplify.
.png)
The LCM is utilized when adding or subtracting rational expressions with different denominators. If the denominators have factors in common, the shared factor only appears once in the LCM.

To add rational expressions with different denominators, factor, multiply each expression so that the denominator is the LCM, add, factor again, and simplify.

To subtract rational expressions with different denominators, factor, multiply each expression so that the denominator is the LCM, convert the subtrahend to its opposite, add, factor again, and simplify.

When adding or subtracting rational expressions, if one denominator is the opposite of the other, multiply one of the rational expressions by -1/-1.

Complex Rational Expressions: Rational expressions that contain one or more rational expressions in their numerator and/or denominator.

Rational Equation: An equation that contains one or more rational expressions.
bottom of page




