top of page
Arithmetic
Contents
Numbers
Operations
Place Values
Digit: A number that names a place value location (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Periods: Groups of three digits separated by commas. Different periods have different names.

Place Value: The value of a digit based on its position in a number.
Place Value Chart: A tool used to identify the position of digits in a number.

Whole Numbers
Natural Numbers: The counting numbers that range from one to infinity.
Whole Numbers: Zero and the natural numbers.

Standard Notation: Numbers are represented by digits with commas located in every three positions.
Expanded Notation: A way to express a number by separating each digit and its place value name. A plus sign "+" separates each digit and place value name.
Word Name: The spoken name of a number.
Number Expanded Notation: An alternative form of expanded notation that uses zeros instead of place value names. A plus sign "+" separates each number in number expanded notation.

Integers
Integers: Whole numbers and their additive inverses.
Additive Inverse: The opposite of a given number. When a number is added to its additive inverse, it equals zero. Since zero is neither positive nor negative, it has no additive inverse and is not a positive or negative integer.

Positive Integers: The natural numbers that are right of zero that range from one to infinity.
Negative Integers: The additive inverses of the natural numbers. Negative integers are found to the left of zero and range from negative one to negative infinity.

Fractions
Fractions: Numbers that are composed of a numerator, denominator, and fraction bar.
Numerator: The number above a fraction bar. A numerator is equivalent to a dividend.
Denominator: The number below a fraction bar. A denominator is equivalent to a divisor.
Fraction Bar: The bar that separates a numerator from a denominator. A fraction bar is equivalent to a division sign "÷" and enacts the same operation.

Improper Fractions: Fractions with an equal or greater number in the numerator than in the denominator.

Complete Fractions: Improper fractions with the same number in the numerator and denominator. Complete fractions are equal to one.

Visual Representations: Portions of a whole visually represent fractions. These representations can be portions of a circle, block, or line.

Equivalent Fractions: Sets of fractions that represent the same value but differ in their numerators and denominators.

There are three ways to test equivalency: the cross-products test, long division, and fraction bars.

Fraction Bars: A visual aid used to determine equivalent fractions.

To produce an equivalent fraction, multiply the fraction of interest by a complete fraction. Multiplying the fraction of interest by a complete fraction is equivalent to multiplying by one.

Simplified Fraction: A fraction with a numerator and denominator that only share one as a common factor.

To simplify a fraction, you must divide the numerator and denominator by their greatest common factor (GCF).
.png)
Sequential Simplifying: A multi-step approach to simplifying a fraction.
Alternatively, any shared factor can be used to divide the numerator and denominator; however, if the greatest common factor is not used, the resulting fraction will require further simplification.

Fractions containing decimals do not typically require simplification.

Any integer or decimal value can be converted into a fraction by putting it over one.

Mixed Numerals
Mixed Numerals: Numbers represented by a whole number and a fraction less than one. Mixed numerals are commonly used to describe the length of measurements made with devices such as rulers or tape measures.
.png)
Mixed numerals represent the sum of a whole number added to a fraction less than one.

Mixed numeral notation is an alternative form of improper fraction notation.


Visual Representations: Mixed numerals are represented by one or multiple complete models and a single incomplete model.

Ratios
Ratio: A quotient that compares two quantities with the same or different units. A ratio can be written in fraction or colon notation.
Rate: A ratio that compares two different kinds of units.
Units: Standardized measurements used to describe the magnitude of a quantity.

.png)
Ratios are written either in colon notation or fraction notation. Ratios use "to" to describe the division bar in word form. Rates use "per" to describe the division bar in word form.


Unlike normal fractions, ratios may not always need to be simplified. Depending on the question and units, simplifying a ratio may result in the loss of statistical and descriptive data.

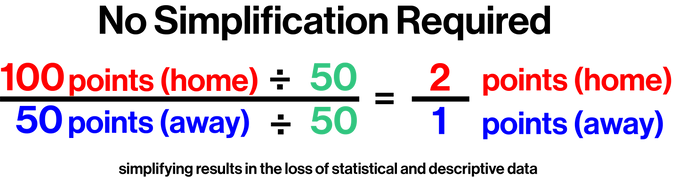.png)
Units can be converted, combined, or eliminated by multiplying by a ratio.
When like units are opposite of each other, they cancel out.

When like units are across from each other, they combine to give an exponent form of the unit.
.png)
Proportion: An equation stating two ratios are equal.

The same processes used to determine if two fractions are equivalent can be used to determine if two ratios are proportional.
Decimals
Decimal Point: The dot that separates digits occupying whole number place values from digits occupying decimal place values.
Decimal Digits: Digits that occupy place values right of the decimal point.
Decimal Place Values: Place values found to the right of the decimal point.



A number can be converted from decimal form to fraction form. The number will have its decimal removed and act as the numerator. The number in the denominator of the fraction will contain one as its leftmost digit and the same number of zeros as the number of decimal places previously occupied.

Fractions can be converted to decimal form by long division.
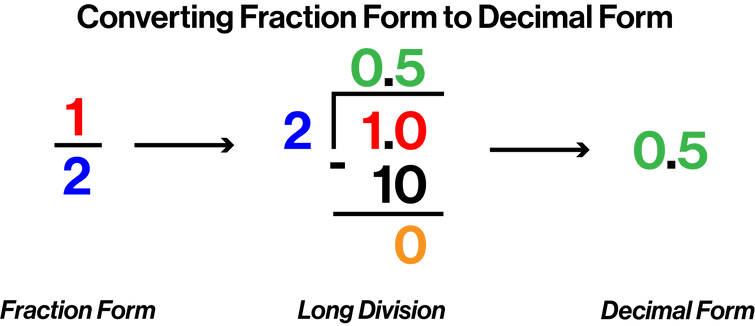.png)
Percentages
Percent Notation (%): Numbers are represented as parts per one hundred. The percent symbol indicates that a number is in percent notation.
.png)
Percent notation can also be expressed in ratio notation, decimal notation, or fraction notation.

Percent notation represents how much of a portion makes up a whole.

Pie Chart: A pie chart is used to show the magnitude of portions that make up a whole. Pie charts visually represent fractions and percentages.

To determine a specific percentage of a number, multiply the number by the decimal form of the percentage.

Negative Numbers
Negative Numbers: Numbers to the left of zero on a number line.

When completing an equation, the amount of negative numbers and their position in the equation affect the sign of the resulting number.

Absolute Value: The distance that a number is from zero on the number line. An absolute value is indicated by a number "x" within absolute value bars |x|. An absolute value is always nonnegative because distance is always nonnegative.

Graphs and Tables
Pictograph: A visualization of data that uses symbols. Each symbol represents a quantity.

Pie Chart: A circular visualization of data in which categories are split into sectors whose sizes correspond to the number associated with each category.

Bar Graph: A visualization of data that uses bars which are proportional in length to the numbers they represent.

Line Graph: A graph in which points represent values. Straight-line segments connect the points.

Histogram: A graph that shows how often certain numbers appear in a set of data.

Stem-and-Leaf Plot: A diagram that displays the frequency distribution of a set of data. The stems are the first digit(s) of the numbers. The leaves are the last digit of the numbers.

Data Table: Data shown in rows and columns.

Frequency Table: A table that displays the number of times a value or values within a range appear in a set of data.

Addition
Addition: The process of combining two or more numbers.
Addend: A number that contributes towards the sum.
Sum: The result of combining addends.


Addition equations should never be completed horizontally since this disregards place values. Instead, addition equations should be changed to a top-to-bottom format.

To test if the sum is correct, check if the inverse operation (subtraction) is also true.

When adding multidigit numbers, the numbers should be aligned. An easy method for aligning multidigit addends is to align them by decimals. After the addends are aligned, any place value without a digit can be filled in with a zero.

Addition begins with the rightmost digits of the addends and moves leftwards.

Carrying: If the sum of two digits is greater than nine, then carrying is required. The digit in the one's place remains, and the digit in the ten's place becomes an additional addend for the place value to the left.


To add or subtract fractions, the fractions must share a common denominator. To find the common denominator, the least common multiple (LCM) of the denominators must be deduced. Then, the fractions are multiplied so each denominator contains the least common multiple.
Multiple: The product of a positive integer of interest multiplied by another positive integer.
Least Common Multiple (LCM): The smallest shared multiple of two or more numbers of interest.

Least Common Denominator (LCD): The least common multiple of the denominators of two or more fractions.


Mixed numerals should be converted into improper fractions before beginning the addition or subtraction process for fractions.
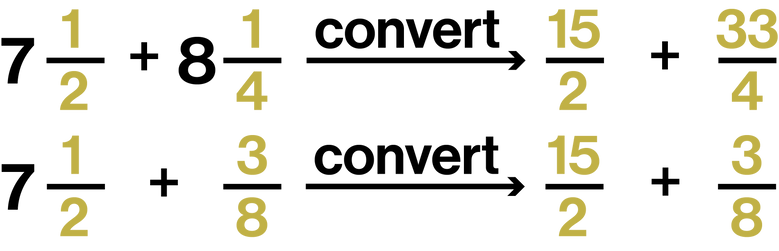
Commutative Law of Addition: When two numbers are added, changing the order of the addends does not affect the sum.

Associative Law of Addition: When three or more numbers are added, changing the order of the addends does not affect the sum.

Subtraction
Subtraction: The process of determining the difference between two or more numbers.
Minuend: The number that is subtracted from.
Subtrahend: The subtracting number.
Difference: The number that results from subtracting one number from another.


Subtraction equations should never be completed horizontally since this disregards place values. Instead, subtraction equations should be changed to a top-to-bottom format.

To test if the difference is correct, check if the inverse operation (addition) is also true.

When subtracting multidigit numbers, the numbers should be aligned. An easy method for aligning multidigit minuends and subtrahends is to align them by decimals. After the minuend and subtrahend are aligned, any place value without a digit can be filled in with a zero.

Subtraction begins with the rightmost digits of the minuend and subtrahend and moves leftwards.

Borrowing: A subtraction process utilized if the minuend digit of interest is smaller than the subtrahend digit of interest. When borrowing, a neighboring place value is reduced by one, and the minuend digit of interest is increased by ten.


Chain Borrowing: When the place value directly to the left of the digit of interest is occupied by a zero, a distant place value must be borrowed from. In this case, the borrowing process occurs multiple times.


To add or subtract fractions, the fractions must share a common denominator. To find the common denominator, the least common multiple (LCM) of the denominators must be deduced. Then, the fractions are multiplied so each denominator contains the least common multiple.


Mixed numerals should be converted into improper fractions before beginning the addition or subtraction process for fractions.

Multiplication
Multiplication: The process of generating groups of numbers. Multiplication can be thought of as repeated addition.
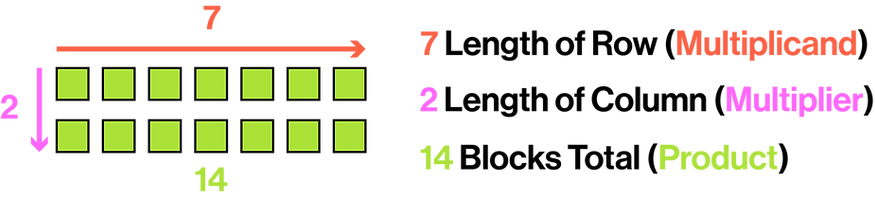
Multiplicand: The number that is multiplied.
Multiplier: The number that amplifies the multiplicand.
Product: The number that results when one number is multiplied by another.

To test if the product is correct, check if the inverse operation (division) is also true.

Whenever zero acts as a multiplicand or multiplier, the product will always be zero.
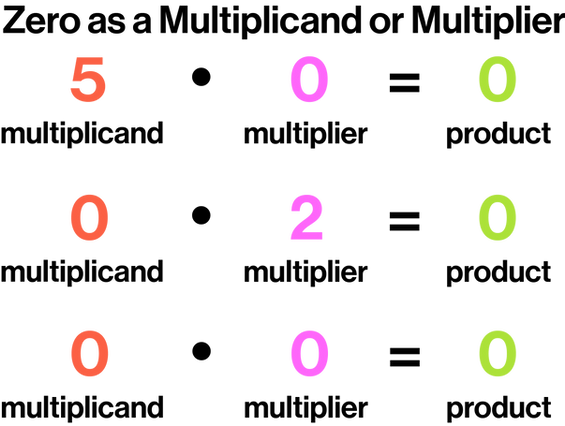
Multiplication can be represented by either the dot symbol or the cross symbol. The dot symbol is preferred since the cross symbol can be confused with the variable "X."

Knowledge of multiplication facts can hasten the speed at which multiplication equations are solved.

Taking advantage of trailing zeros can reduce the multiplication process.
Leading Zeros: Zeros that do not have any nonzero digits ahead of them.
Sandwiched Zeros: Zeros that are between nonzero digits.
Trailing Zeros: Zeros that do not have any nonzero digits behind them.

Trailing zeros can be ignored during the multiplication process. Once the multiplication process is complete, the number of trailing zeros can then be used to move the decimal to the correct position to solve for the final product.

Decimal place trailing zeros can be ignored during the multiplication process; however, decimal place trailing zeros do not contribute to the movement of the decimal when solving for the final product.

Converting the multiplicand, multiplier, or both into their number expanded notion can result in a series of easier multiplication equations. Then, the products of these equations can be added. The sum of the products is equivalent to the product of the original multiplication equation.
.png)
.png)
.png)
Long multiplication is especially useful for solving multiplication equations containing large numbers or decimal values.
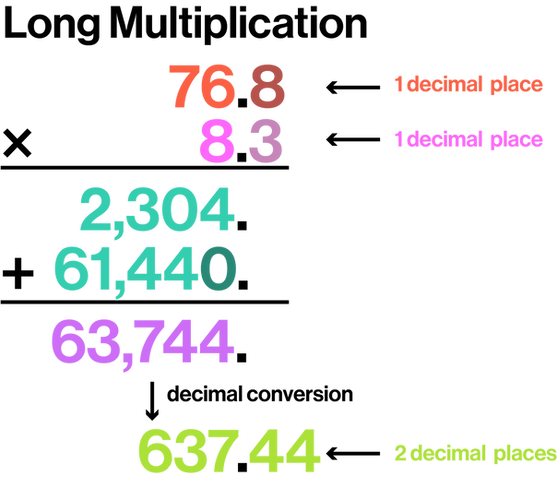
Multiplication equations can be solved by repeated addition of the multiplicand or multiplier.
.png)
.png)
When fractions are multiplied, the numerators and denominators are multiplied directly across.

Mixed numerals should be converted into improper fractions before multiplying.

Commutative Law of Multiplication: When two numbers are multiplied, swapping the multiplicand and multiplier does not affect the product.

Associative Law of Multiplication: When three or more numbers are multiplied, changing the order of the numbers does not affect the product.

Distributive Law of Multiplication: Multiplying a number by a sum or difference is equivalent to multiplying each component separately, then adding or subtracting.

Division
Division: The process of splitting a number into groups. Division can be thought of as repeated subtraction.
Dividend: The number that is split.
Divisor: The number that splits the dividend.
Quotient: The number that results when one number is divided by another.


To test if the quotient is correct, check if the inverse operation (multiplication) is also true.

Knowledge of multiplication facts can be an alternative method for determining the quotient. This can be done by rearranging the division equation into its inverse operation, multiplication.

When numbers can't be evenly divided, the quotient will contain a remainder, a fraction, or a decimal.
Remainder: The leftover value after division occurs.


A quotient that contains a remainder can be checked using the inverse operation of division (multiplication) and addition to account for the remainder.

Instead of a remainder, the quotient may contain a fraction or decimal.

Long division is a process that is especially useful for solving equations containing large numbers or decimals.

Division may result in a non-terminating decimal or a decimal that reaches distant place values. Rounding these quotients to the thousandth place when possible gives a reasonable estimate of the actual value.

To divide fractions, multiply by the reciprocal of the divisor.
Reciprocal: The reciprocal of a fraction can be found by swapping the numerator and denominator. If the reciprocal is multiplied by the original fraction, the product is always one.

To divide mixed numerals, convert them into improper fractions.

Complex Fractions: Fractions in which one or more fractions occupy the numerator and/or the denominator. Complex fractions are solved by multiplying by the divisor's reciprocal.
.png)
When zero is a divisor, it will always result in an undefined or indeterminate quotient. When dividing by zero, the logical consequence would be a quotient of zero; however, the inverse operation would then result in any desired number. Thus, zero is excluded as a divisor and always results in an undefined or indeterminate quotient.

Radicals
Radical Notation: A root represented by a radicand under a radical.
Root: A number multiplied by itself "X" times, based on the index, that equals the radicand. Roots can either be positive or negative.
Radical (√): Indicates that only the positive root should be solved for.

Square Root: "b" is a square root of "a" if b^2 = a. Many basic square roots can be determined by memorizing multiplication facts.

.png)
Powers of 10
Powers of 10: Any of the integer powers of the number ten.

Multiplying or dividing a number by a power of 10 can be thought of as moving the decimal to the left or right a certain number of times, depending on the number of leading or trailing zeros.

Scientific Notation: A notation that is especially useful for presenting large or small numbers in a reduced format.

Factorization
Factor: A positive integer that divides a larger positive integer evenly, leaving no remainder.

If a number is a factor of a product, it also means that the product is a multiple of the factor.

Factorization: The expression of a number as a product of two or more factors.

Only positive integers are considered when determining a number's factors.

Being able to determine all the factors of a number is essential. This skill makes multiplying, dividing, and simplifying fractions easier.
.png)
Factors can be determined by either multiplication or division.

The product itself and one will always be factors. One is the multiplicative identity and always equals the number it is multiplied by.

Prime Numbers: Numbers that only have two factors: one and itself. Two is the only even prime number.

Composite Numbers: Numbers that have more than two factors.

Multiplication Chart: A tool that visualizes the multiples of numbers ranging from one to twelve. Additionally, multiplication charts can be used to determine the factors of a number.

Divisibility Tests: Tests that circumvent division and allow one to check if an integer is divisible by 2, 3, 5, 6, 9, or 10. These tests assist in determining the factors of a number.

Prime Factorization: The sequential factorization of a composite number and its factors that results in a unique set of prime numbers. The prime numbers produced by prime factorization, when multiplied, equal the original composite number.

Factor Tree: A branching factorization method that involves factoring composite numbers until only prime numbers remain.

Prime factorization can be used as a method to find the least common multiple for a set of numbers.

Prime factorization can be used as a method to simplify fractions.

Order of Operations
Order of Operations: The steps taken to calculate an equation correctly.


Bracketing Method: A way to manage multiple numbers and operations in an equation by using brackets to complete the equation in a step-by-step manner, rather than attempting to solve the equation in a single step.

bottom of page






